无约束优化
无约束优化
无约束优化：
无约束优化要求求解
线性回归
试图学得一个线性模型，通 过因素、属性或者说特征的线性组合，来尽可能准确地预测实 际输出值，即寻求线性函数
基于均方误差最小化来进行模型求解的方法也被称为**“最小二乘法”(least square method)**。
带正则项的线性回归
**
其中
岭回归： 为了平衡模型的拟合性质和解的光滑性，还可以用
通过设置合适的
无约束优化最优性条件
一阶必要条件（FONC）
**一阶必要条件：*设
$$
\nabla f(\boldsymbol{x}^)=0
$$
利用一阶泰勒展开式证明即可。
注意：
- 驻点（平稳点）是一阶导数为
的点。 - 极大值、极小值、鞍点都可能是平稳点。
二阶必要条件（SONC）
**二阶必要条件：*设
$$
\nabla f(\boldsymbol{x}^)=0\text{且}\nabla^2f(\boldsymbol{x}^*)\text{是半正定}
$$
证明：如果非半正定，则存在
二阶充分条件（SOSC）
设
证明：根据泰勒级数，领域内任意一个值都要比它更大，即
$$
f(x^+\alpha d^)=f(x^)+\frac12\alpha^2d^T\nabla^2f(x^)d+o(\alpha^2)>f(x^*)
$$
**注意：**SOSC不是必要条件。
凸函数最优性条件
凸优化能保证驻点为局部极小点，也就是全局极小点。
无 约 束 凸 优 化 : 设 凸 函 数
证明：
$$
f(x)-f(x^)\geq\nabla f(x^)(x-x^*)=0
$$
因此
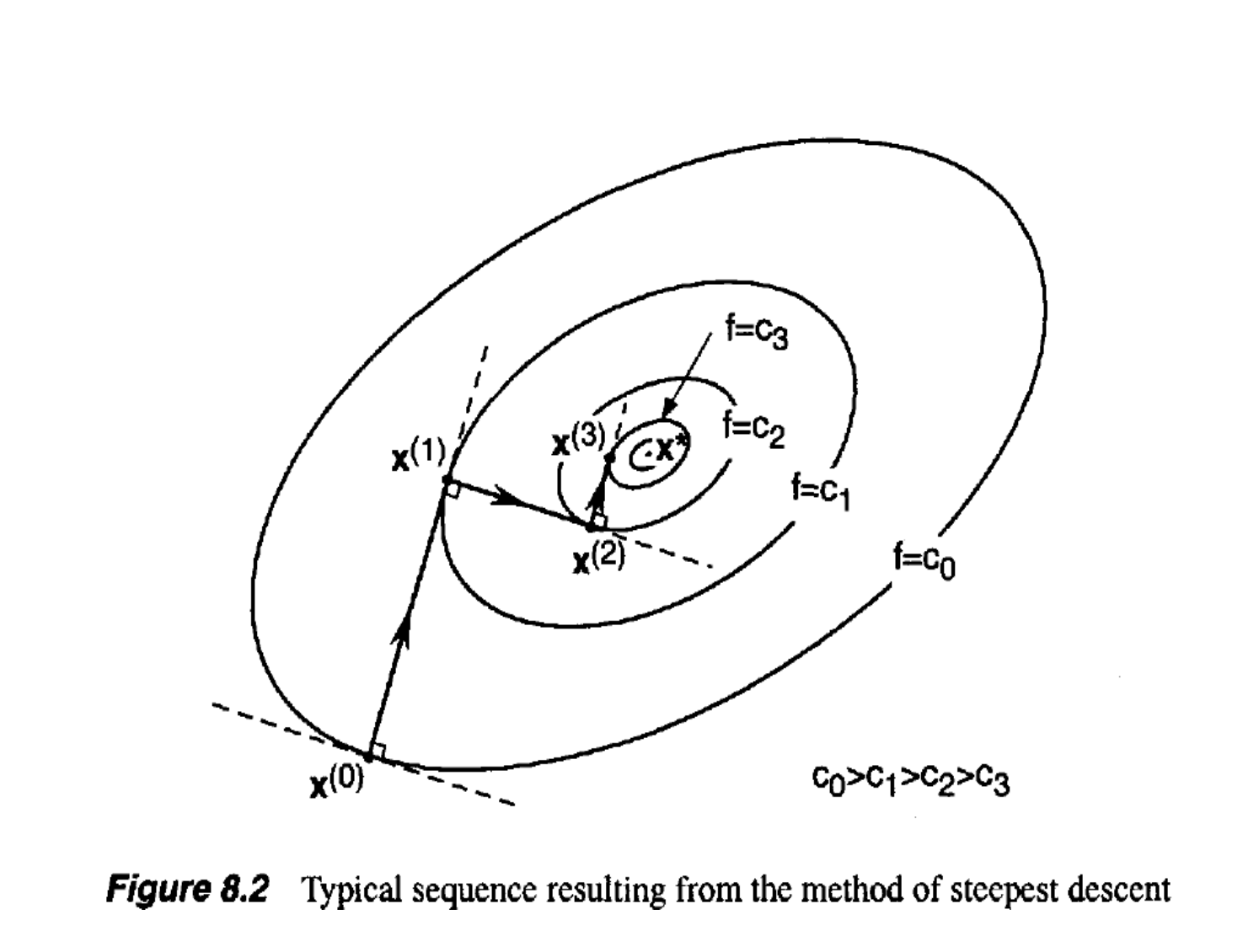
下降法
难以求解
步骤：
- 首 先 确 定 目 标 函 数
的 极 小 点 的 一 个 初 始 估 计 : 。 - 然后按照一定规则产生一个下降方向
。 - 再沿方向
，求得下一个迭代点 即在射线 上确定一个新点： ，使得 ，其中 称为步长因子。 - 若满足停机条件则输出
，否则 ，转到第二步
注意：机器学习中
下降方向
下降方向：设函数
因此
负梯度
确定步长因子
- 固定步长
- 衰减步长因子：
，其中 - 精确/近似线搜索：
，则 。
精确线搜索
性质：由于
换句话说，在精确线搜索中，
近似线搜索
充分下降条件 (Amijo条件)
选择常数
回溯线搜索
为了满足我们可以以大的步长开始，并且通过恒定的缩减因子将其减小至满足充分下降条件。因为该算法沿着下降方向回溯，所以被称为回溯线搜索。
曲率条件
Amijo条件不足以保证收敛到局部极小值。非常小的步长可以满足第一个条件，但可能致过早收敛。
曲率条件（第一WOLF条件）
其中
强曲率条件（第二WOLF条件）
停机条件
限制迭代次数
一阶方法
共轭梯度法
**共轭定义：**设
二次型下的共轭方向法
针对
令
再由 FONC 得
证明：由于方向
……
找出一组
**共轭梯度法：**利用上一次搜索方向和目标函数在当前迭代点的梯度向量之间的线性组合构造一个新方向，即
初始方向：
时：
那么
时 : 设 第 次 的 方 向 为 , 第 次 的 梯 度 是 ，设
为了使
因此
对于
二阶方法
问题：假设
牛顿法
算法流程：
选定初始点
通过
计算 。 确定下一个迭代点
是否满足停机规则。
拟牛顿法
秩一修正法：构造
由于
再根据拟牛顿条件