一维无约束优化

主要讨论一维（单峰函数）的最小化问题算法

$\min f(x),x\in \mathbb{R}$

单峰函数：如果一维函数在定义域区间上有唯一局部极小点 ，则称为区间上的 单峰函数（unimodel function）。

性质：在上任取两点且

，则极小值一定位于之间
，则极小值一定位于之间

等比例压缩法

每次在当前区间按等比例取两个点

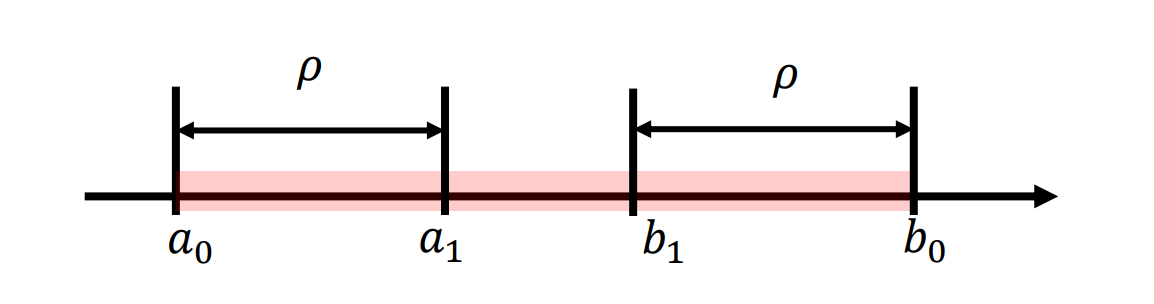
每次迭代后区间变成原来的倍，故次迭代后总压缩比为，其中每次压缩要取两个点重新计算函数值并比较，所以调用次数为。

黄金分割法

在等比例压缩法的基础上将压缩比设置为，好处是每一次产生的新区间中总包含了上一次计算的一个点，使得下一次运算时该店可以重复使用。

总压缩比为，调用次数为（第一次还是要算两个点，其余每次只多算一个点）。

斐波那契法

前面两种方法是 要求达到目标压缩比，能否 给定迭代次数 ，但允许 的值动态改变，使得 次迭代后的压缩比最小，并且仍然每次只增加对一个点的目标函数进行计算。

即满足

$\rho_{k+1}(1-\rho_k)=1-2\rho_k\\\rho_{k+1}=1-\frac{\rho_k}{1-\rho_k}$

转化成求：

$\min (1-\rho_1)(1-\rho_2)\dots (1-\rho_n)\\s.t.\rho_{k+1}=1-\frac{\rho_k}{1-\rho_k},k=1,\dots, N-1\\0\le \rho_k\le\frac{1}{2},k=1,\dots, N-1$

满足以下序列的解即为改最优化问题的最优解：（证明过程P78）

$\rho_{1} = 1-\frac{F_{N}}{F_{N+1}},\quad\rho_{2} = 1-\frac{F_{N-1}}{F_{N}},...,\rho_{k} = 1-\frac{F_{N-k+1}}{F_{N-k+2}},... ,\rho_{N} = 1-\frac{F_{1}}{F_{2}}$

注意：在第次迭代时，此时两个点重叠，需要加上一个扰动量，即，因此，对于极小点所在的区间的压缩比可能是：或

总压缩比为

在趋于无穷时，黄金分割法实际上和斐波那契法有着相同的压缩比

二分法

需要目标函数连续可微，

Step 1 确定初始区间的中点
Step 2 计算函数在中点的导数。如果，说明极小点在左侧，压缩下一次的搜索区间为。如果 ,说明较小点位于右侧，下一次迭代玉缩区间为。最后，如果 , 说明是极小点。
Step 3 按照第2步迭代，根据的大小来压缩区间，直到区间大小小于预期要求或者 (由于数值误差，后者一般不会出现，所以停机条件会要求区间大小在某一约束内)

方法	压缩比	调用次数
等比例压缩法
黄金分割法
斐波那契法
二分法		\

确定初始搜索范围

bracket_ minimum算法

牛顿搜索方法

若在二阶连续可微，则

$f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac12f''(x_0)(x-x_0)^2+o(|x-x_0|^2)$

可以利用

$q(x)=f(x^k)+f^{\prime}(x^k)(x-x^k)+\frac12f^{\prime\prime}(x^k)(x-x^k)^2$

作为在附近的近似

牛顿法利用的极小点作为，即下次迭代点，即

$x^{(k+1)}=x^{(k)}-\frac{f^{\prime}(x^{(k)})}{f^{\prime\prime}(x^{(k)})}$

牛顿法求解方程

牛顿法迭代过程中并不需要计算，却能找到的点。因此，令，牛顿法也能求解方程，迭代方程为

$x^{(k+1)}=x^{(k)}-\frac{g(x^{(k)})}{g^{\prime}(x^{(k)})}$

有可能会因为不够小失效

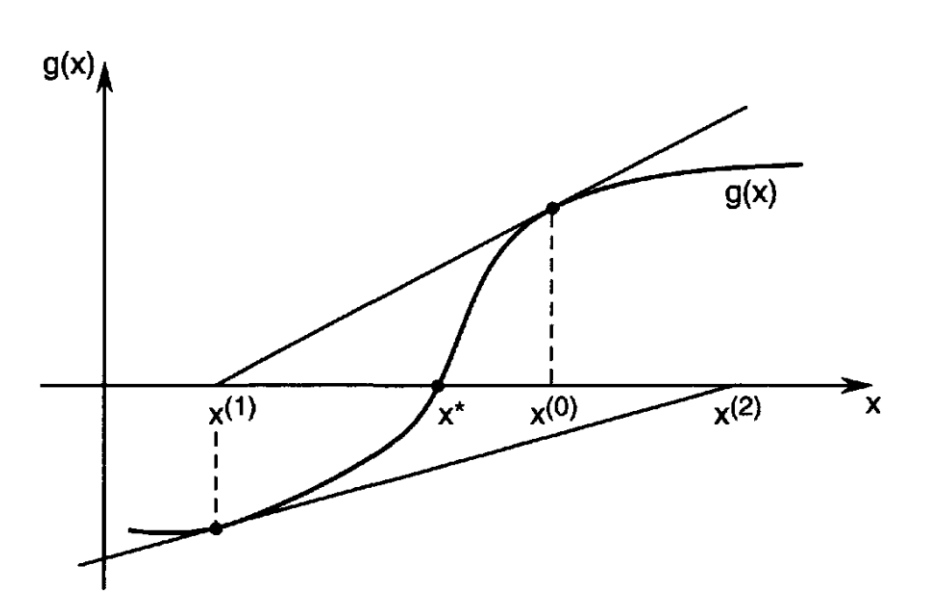
割线法

利用不同点处的一阶导数近似二阶导数

$x^{(k+1)}=x^{(k)}-\frac{x^{(k)}-x^{(k-1)}}{f'(x^{(k)})-f'(x^{(k-1)})}f'(x^{(k)})$

由于每次迭代使用了两个点的信息，初始点需要有两个和。

二次拟合搜索

不计算一阶导数的情况下，求解上述一维最优化问题。

令：

$X=\begin{bmatrix}\left(x^k\right)^2&x^k&1\\\left(x^{k-1}\right)^2&x^{k-1}&1\\\left(x^{k-2}\right)^2&x^{k-2}&1\end{bmatrix},y=\begin{bmatrix}f(x^k)\\f(x^{k-1})\\f(x^{k-2})\end{bmatrix},\text{则}A\begin{bmatrix}a\\b\\c\end{bmatrix}=y$

由克拉默法则 , b, 其中为用 y取代的第 1 和第 2 列后的矩阵。

实际上，我们并不需要计算参数。考虑二次函数的最小值为，我们只需要计算